Oppervlakte cirkel berekenen

Je kunt de oppervlakte van een cirkel berekenen door uit te gaan van de diameter hiervan, die we ook wel de doorsnede noemen. Het getal ‘pi’ speelt hierbij een belangrijke rol. Het is een cijfer met enorm veel getallen achter de komma, waardoor je het best gebruik kunt maken van onze tool. lees meer

Straal en oppervlakte berekenen

Wil je de oppervlakte van een cirkel berekenen? Het is een berekening die je waarschijnlijk niet zomaar uit je hoofd kunt maken. Dankzij onze online berekening kun je de oppervlakte van een cirkel eenvoudig berekenen, je hebt daar slechts de straal van de cirkel voor nodig.

Een cirkel is een bijzondere figuur, waarbij ieder punt op de rand dezelfde afstand heeft tot het middelpunt. Die voorwaarde is van belang op het moment dat je de oppervlakte van een cirkel wilt berekenen, aangezien je er aan de hand daarvan vanuit kunt gaan dat alle vier de kwarten van de cirkel even groot zijn. De afstand vanaf de rand tot aan het midden van de cirkel noemen we de straal, daar komen we zo nog even op terug voor het berekenen van de oppervlakte van de cirkel. De oppervlakte gaat om de binnenkant van de cirkel, houd er rekening mee dat je dit niet verwart met de omtrek. De omtrek van de cirkel staat voor de rand, die kun je op een andere manier berekenen. Uiteraard is ook daar een formule voor beschikbaar, zodat je daar niet zelf mee aan de slag hoeft.

Wil je de oppervlakte van een cirkel berekenen? Daarvoor maken we gebruik van een paar verschillende stappen. In principe zou je een cirkel op een vlak met blokjes kunnen rekenen, waarbij ieder kwart van de cirkel precies in 4 gelijke blokjes valt. Je hebt dan een vel van 4 x 4 blokjes nodig, er zijn er in totaal 16 aanwezig. Wat je op die manier kunt zien is dat een van de vierkanten van 2 x 2 blokjes staat voor een kwart van de cirkel, waarbij je de oppervlakte kunt aanduiden als r x r. Die r staat voor de lengte van 2 blokjes in de horizontale richting, net als 2 blokjes in de verticale richting. De oppervlakte van de 2 x 2 blokjes kunnen we schrijven als r kwadraat. Je kunt bovendien nagaan dat er in totaal 4 van die blauwe vlakken aanwezig zijn. Het vak dat je nodig hebt om de cirkel te kunnen tekenen heeft dus een oppervlakte van 4 x r kwadraat.

Om de oppervlakte van een cirkel te kunnen berekenen dienen we een factor te nemen kleiner dan 4, omdat de cirkel immers kleiner is dan het vierkante blok dat je nodig hebt om die te kunnen tekenen. Het dient een getal tussen de 3 en de 4 te zijn. Het blijkt het getal ‘Pi’ te zijn. Pi staat voor een getal dat we kunnen afronden op 3,14, dat precies geschikt blijkt te zijn om de optrek van een cirkel te berekenen.

We kunnen de oppervlakte van een cirkel berekenen door gebruik te maken van het getal Pi, dat we kunnen aanduiden als π. Pi is afgerond 3,14, eigenlijk is het een getal met een groot aantal getallen achter de komma. Het zou hier niet van toegevoegde waarde zijn dat getal helemaal uit te schrijven, in de formule voor het berekenen van de oppervlakte van een cirkel maken we daar uiteraard wel gebruik van. Pi staat voor het aantal keren dat de diameter van de cirkel op de rand past, wanneer je die er als het ware omheen zou buigen. De diameter van de cirkel is de doorsnede, die is twee keer langer dan de straal. Je kunt er dus vanuit gaan dat de straal van een cirkel zo’n 6,28 keer op de rand past, de diameter van de cirkel past er 3,14 keer op.

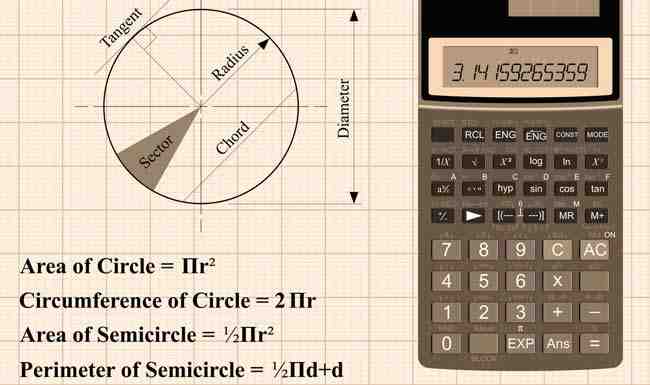
Formule voor de oppervlakte van een cirkel

Benieuwd naar de formule om de oppervlakte van een cirkel te berekenen en enkele voorbeelden zien hoe we tot de uitkomst komen? De formule voor het berekenen van de oppervlakte van een cirkel ziet er als volgt uit:

Oppervlakte cirkel = π x straal x straal = π x straal in het kwadraat

We kunnen de oppervlakte van een cirkel berekenen, bijvoorbeeld op het moment dat je wil weten hoeveel vierkante meter graszoden je nodig hebt om een rond grasveld met een diameter van 12,4 meter te vullen. Het is verstandig om het geheel af te ronden op 2 decimalen, aangezien je anders zal merken dat je enorme getallen krijgt, waarmee je uiteindelijk niet goed kunt werken.

Om de oppervlakte van de cirkel te berekenen hebben we in ieder geval de straal nodig, die moeten we immers invullen in de formule. De straal is de helft van de diameter, aangezien het gaat om de rand van de cirkel tot aan het middel daarvan. Bij een diameter van 12,4 is er sprake van een straal van 6,2 meter, dat valt gemakkelijk uit te rekenen. Dat betekent dat we die 6,2 meter in de formule kunnen invoeren:
Oppervlakte cirkel = π x 6,2 x 6,2 = 120,76 vierkante meter

Dat betekent dat je voor een grasveld met een diameter van 12,4 meter dus ruim 120 vierkante meter aan gras nodig hebt. Uiteraard moet je er in dat geval wel vanuit kunnen gaan dat het grasveld inderdaad de vorm van een cirkel heeft, deze dient netjes rond te zijn. Wil je dat op voorhand met zekerheid bepalen? Het is dan slim om de diameter op een willekeurig punt op te meten. Aan de hand daarvan bepaal je het middel (de helft van de diameter). Op dat punt steek je een stokje in de grond met een touwtje met 6,2 meter lengte. Je komt dan precies op de rand uit, waar je begonnen bent met meten. Loop met dit touwtje een rondje om na te gaan of het inderdaad gaat om een cirkel, de afstand van de rand tot aan het midden zou dan overal gelijk moeten zijn. Merk je dat dit inderdaad het geval is? Dan kun je de oppervlakte van de cirkel berekenen aan de hand van de methode die we hierboven hebben beschreven, bijvoorbeeld om na te gaan hoeveel gras je nodig hebt om het gehele veld te vullen.

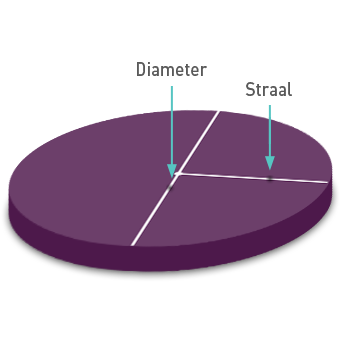
Straal van een cirkel

Het is voor het berekenen van de oppervlakte van de cirkel van groot belang dat je de straal kent. Gelukkig kun je die gemakkelijk opmeten, aangezien je daarvoor geen gebogen afstanden hoeft op te nemen. Het is vooral van belang om het middel van de cirkel te bepalen, iets dat je kunt doen aan de hand van de diameter. Indien je te maken hebt met een cirkel kun je op een willekeurig punt beginnen met meten en naar de overkant van de cirkel lopen. De diameter van een cirkel is op ieder punt hetzelfde. Heeft het grasveld op een bepaald punt een diameter van 12,4 meter? Dat zal 10cm naar links of naar rechts dan ook zo zijn, anders is het immers geen cirkel. Dat betekent dat het niet uitmaakt waar je begint met meten op het moment dat je achter de diameter wilt komen. Je kunt de oppervlakte van de cirkel berekenen aan de hand van de diameter, omdat je op basis daarvan na kunt gaan hoe lang de straal is die je daarvoor kunt gebruiken.

Straal cirkel

Om de oppervlakte van een cirkel te berekenen heb je de straal nodig, die je kunt berekenen op het moment dat je de diameter van de cirkel kent. De straal van de cirkel is half zo klein als de diameter. Zodra je de diameter hebt is het voldoende om die precies door 2 te delen, je komt op die manier immers uit in het midden van de cirkel. Het is de moeite waard om de straal daarna in een aantal andere richtingen tot op de rand op te meten. Op die manier kun je nagaan of er inderdaad sprake is van een cirkel. De straal zou dan steeds dezelfde lengte moeten aangeven.

Je kunt op basis van de straal eenvoudig online de oppervlakte van een cirkel berekenen, de formule zit niet moeilijk in elkaar. Vind je het lastig om een kwadraat uit te rekenen of wil je er zeker van zijn dat je de juiste berekening maakt van de oppervlakte van een cirkel? Je kunt online de formule voor het berekenen van de oppervlakte berekenen, wij nemen je het rekenwerk graag uit handen. Het is voldoende om zelf de diameter van een cirkel op te meten of te bepalen en aan de hand daarvan aan te geven wat de straal is. Wij berekenen vervolgens de oppervlakte van de cirkel, zodat je precies weet hoeveel gras je nodig hebt om het veldje op te vullen of je weet wat de oppervlakte is.

Nieuws over Straal en oppervlakte

Uitgelegd: Hoe bereken je nu de oppervlakte van een cirkel

Ben je benieuwd hoe je de oppervlakte van een cirkel kunt berekenen? Dan ben je hier aan het juiste adres! Het berekenen van de oppervlakte van een cirkel is een belangrijke vaardigheid in de wiskunde en kan in veel situaties van pas komen. Of je nu een wiskundeles hebt, een klus in de tuin doet of gewoon je nieuwsgierigheid wilt bevredigen, het is handig om te weten hoe je dit kunt doen.

» Lees het volledige bericht

Oppervlakte berekenen verantwoordelijkheid van makelaar

Wie is er verantwoordelijk als de woning niet juist blijkt te zijn opgemeten? Het kan een kostbare fout zijn bij de verkoop van een huis, zo bewijst een zaak uit Den Bosch. Een verkoper schakelde een makelaar in, die een meetfout maakte.

» Lees het volledige bericht

Heerlijk huis met unieke vormen: oppervlakte berekenen blijkt lastig

Veel huizen zijn rechttoe-rechtaan en zijn daardoor weinig spannend. Dat geldt niet voor villa De Vreemde Eend in Rijkerswoerd. Het is letterlijk en figuurlijk een vreemde eend in de bijt, bijvoorbeeld dankzij de woonkamer in een cirkel.

» Lees het volledige bericht